Kartprojektioner och förvrängningar
Kartritare arbetar vid framtagandet av nya kartor alltid utgående från bestämda projektioner. Ytan av ett klot kan i sin helhet inte plattas ut till 2 dimensioner utan att klotets mönster blir förvrängt. Samma gäller när jordens klotformade yta skall projiceras till en karta. Då väljer man ett projiceringssätt som styr förvrängningarna (uttöjningarna) till de områden som är minst viktiga på kartan.
En vanlig projektion är Mercator, där polerna "viks upp" så att ytan blir en cylinder. Sedan vecklar man ut cylinderns mantelyta till en platt karta:
Mercator kartan är ofta använd världskartor. På den här kartan är norr uppåt överallt, och syd är nedåt. Hela den övre kanten motsvaras av nordpolen och den nedre av sydpolen. Dessa områden är alltså uttöjda och utgör kartans största förvrängningar. Vid ekvatorn finns inga förvrängningar.
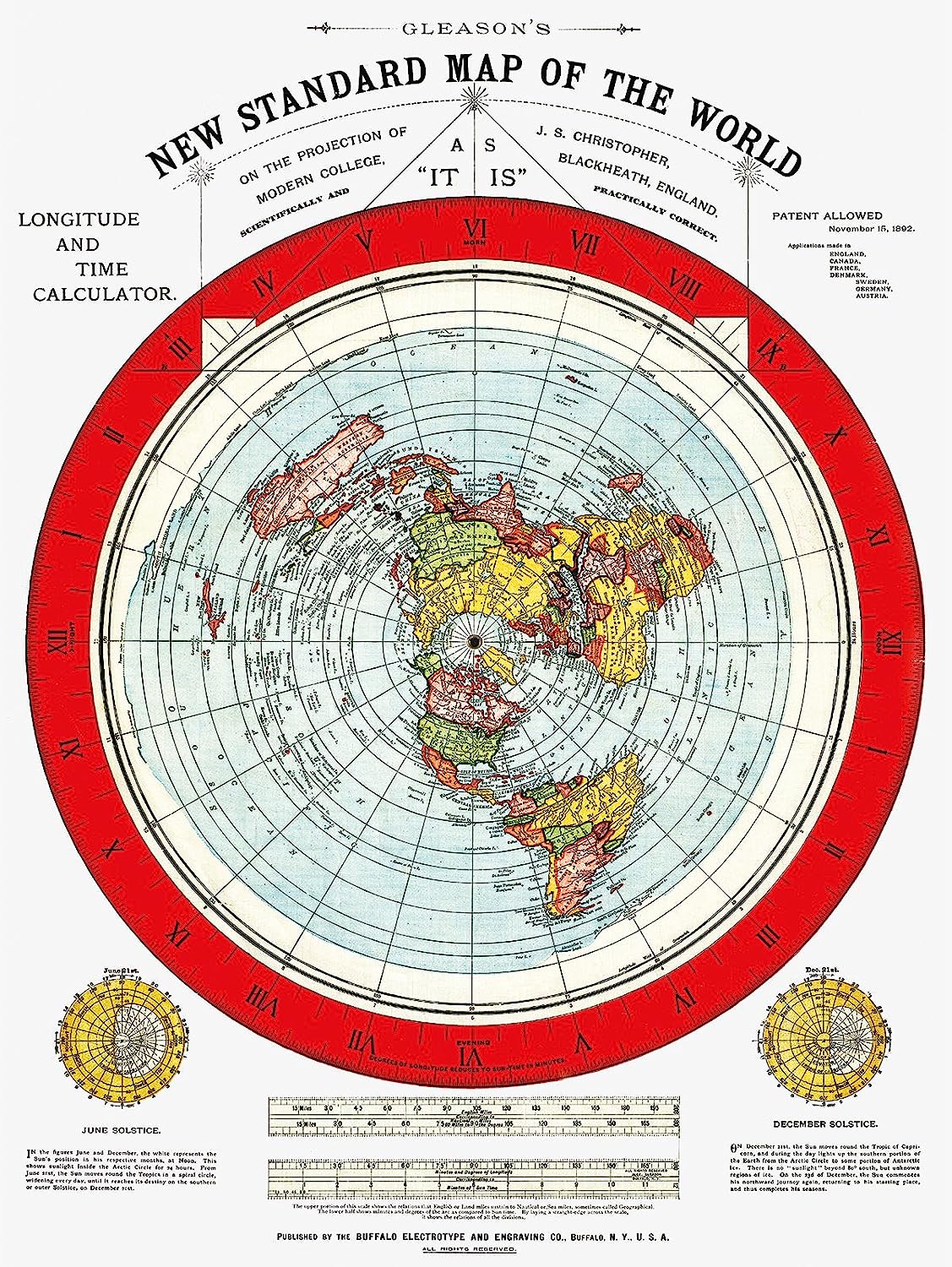
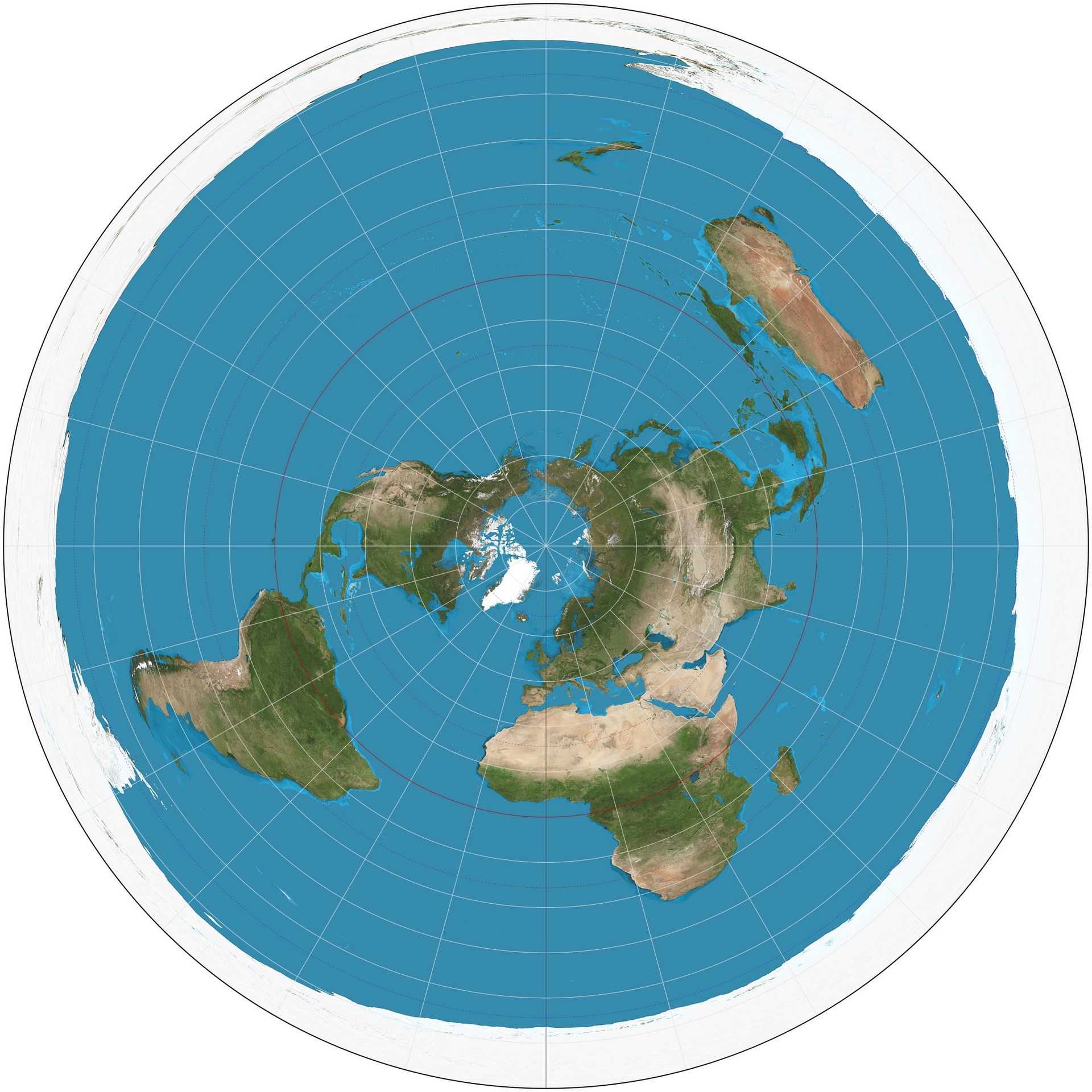
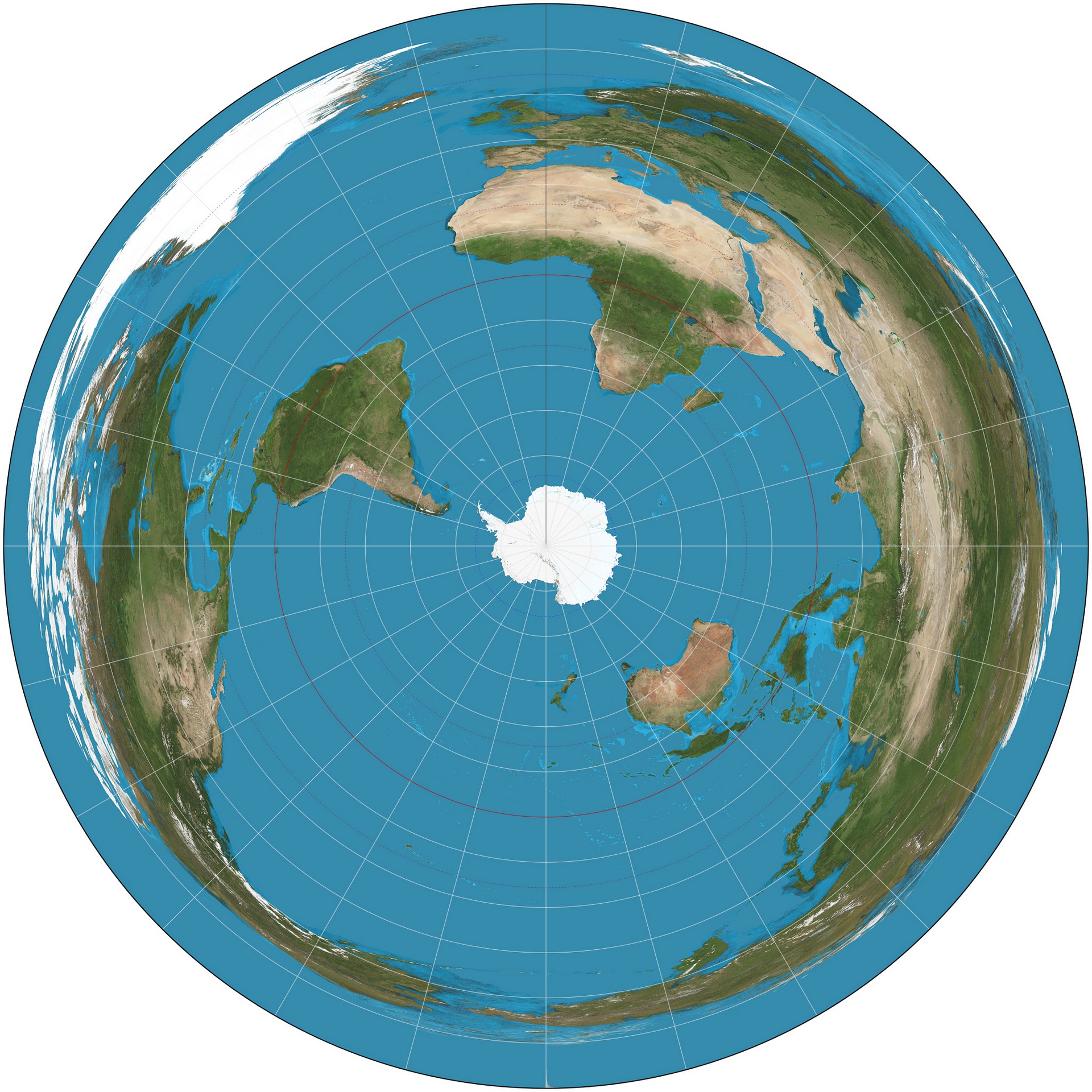
En annan mindre vanlig projektion är Azimutal ekvidistant och tar fasta på en punkt på jorden som sedan blir kartans mitt. Hela klotet viks sedan upp från motsatta polen så att man får en rund karta där den motsatta polen utgör hela den yttre kanten. Ekvidistant betyder att avståndet mellan vilka två punkter som helst längs en meridian (linjerna som strålar ut från centerpunkten) är enligt en jämn skala.
Två exempel på Azimutala projektioner finns nedan. Den första är med nordpolen som centerpunkt och den andra med sydpolen som centerpunkt:
Här illustreras respektive projektion med de förvrängda områdena målade med orange färg:
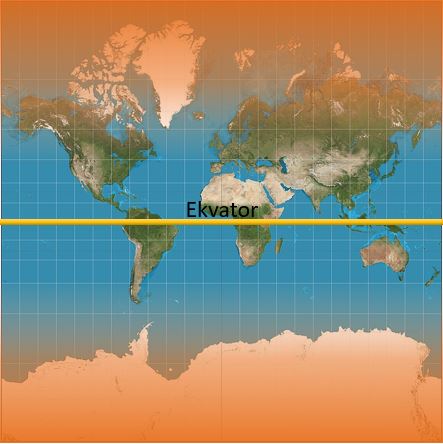
Mercator med förvrängningsområden. Polarområdena är stretchade framförallt i höjdled, så att t ex Grönland verkar vara nästan lika stort som Afrika eller Sydamerika.
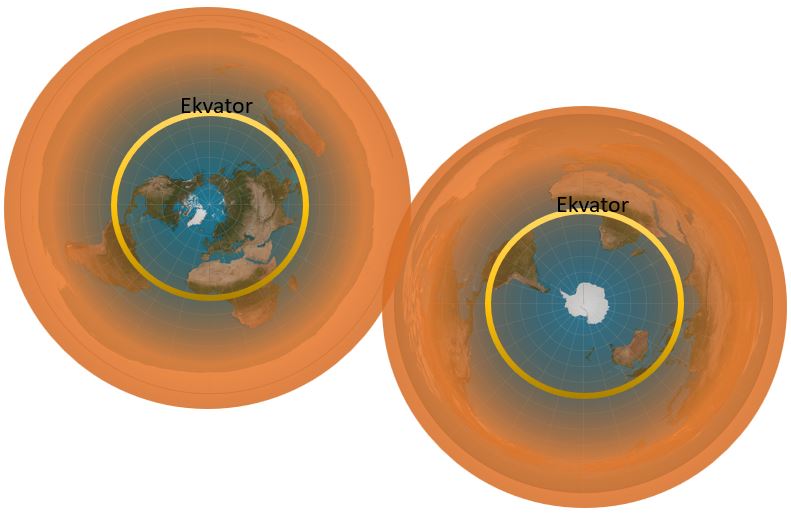
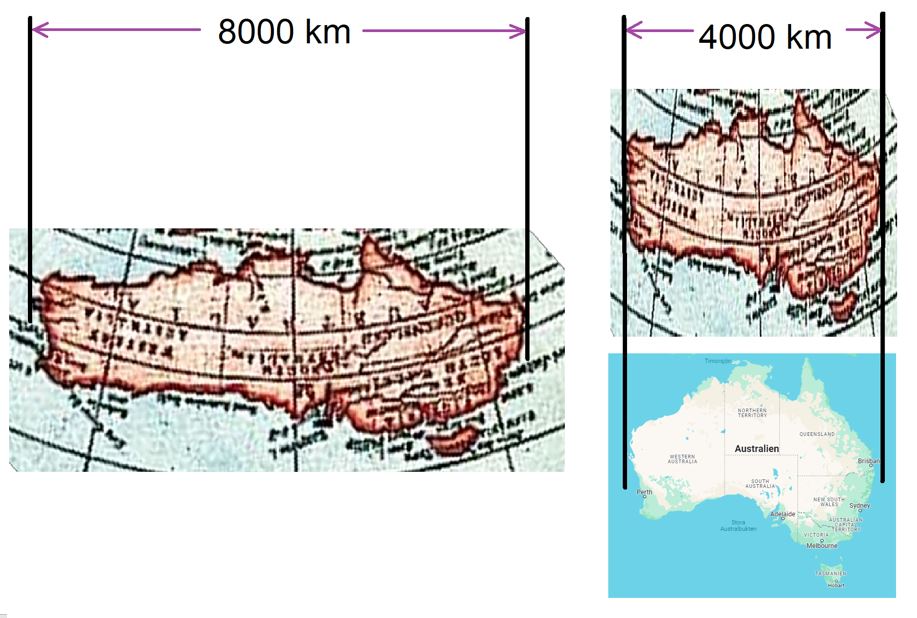
Azimutal nordpol resp. sydpol med förvrängningsområden. Det är bara i princip centerpunkten och ca 1/3 utåt som inte är förvrängt. Redan vid ekvatorn är förvrängningarna stora, för att sedan mot ytterkanten bli dramatiska.